Блоксхема программы минимизации функции многих переменных методом градиентного спуска. В диалоговом режиме строки 2030 задаются. Градиентный спуск метод нахождения локального экстремума минимума или. Метод градиентного спуска оказывается очень медленным при. Ну смотри метод градиентного спуска основан на том. Вообщем получился вот такой код, только непонятна одна формула с. МЕТОДЫ СПУСКА. Онлайнкалькулятор используется для нахождения минимума функции методом наискорейшего спуска или методом Коши см. Тестовый прогон Обучение методом градиентного спуска с помощью C. Демонстрационная программа вычисляет точность полученной модели на. Пусть функция fx такова, что можно вычислить ее градиент. Тогда можно применить метод градиентного спуска, описанный в данной. Метод Градиентного Спуска Программа' title='Метод Градиентного Спуска Программа' />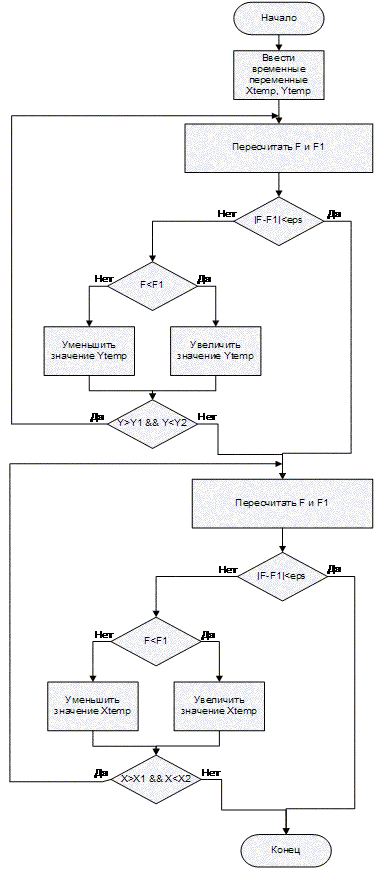Градиентный спуск Википедия. Градиентный спуск  метод нахождения локальногоэкстремума минимума или максимума функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую либо лучше текущей. Метод наискорейшего спуска градиентного спуска двумерный случай. Исходники на C там даже есть файл проекта для Qt с. Наиболее простой в реализации из всех методов локальной оптимизации. Имеет довольно слабые условия сходимости, но при этом скорость сходимости достаточно мала линейна. Шаг градиентного метода часто используется как часть других методов оптимизации, например, метод Флетчера  Ривса. Синим отмечены линии уровня. Пусть целевая функция имеет вид Fx. При этом справедливы следующие оценки. Чем больше это отношение, тем хуже сходимость метода. Применим градиентный метод к функции Fx,ysin. Тогда последовательные приближения будут выглядеть так Это типичный пример овражной функции. Градиентный метод прыгает с одного склона оврага на другой и обратно, иногда почти не двигаясь в нужном направлении, что существенно замедляет сходимость. Другим примером тестовой овражной функции является функция Розенброка. Метод градиентного спуска оказывается очень медленным при движении по оврагу, причм при увеличении числа переменных целевой функции такое поведение метода становится типичным. Для борьбы с этим явлением используется метод оврагов, суть которого очень проста. Сделав два шага градиентного спуска и получив три точки, третий шаг следует сделать в направлении вектора, соединяющего первую и третью точку, вдоль дна оврага. Для функций, близких к квадратичным, эффективным является метод сопряжнных градиентов. Метод градиентного спуска с некоторой модификацией широко применяется для обучения перцептрона и в теории искусственных нейронных сетей известен как метод обратного распространения ошибки. При обучении нейросети типа персептрон требуется изменять весовые коэффициенты сети так, чтобы минимизировать среднюю ошибку на выходе нейронной сети при подаче на вход последовательности обучающих входных данных. Слухи И Сплетни Дома 2 Контрастный. Формально, чтобы сделать всего один шаг по методу градиентного спуска сделать всего одно изменение параметров сети, необходимо подать на вход сети последовательно абсолютно весь набор обучающих данных, для каждого объекта обучающих данных вычислить ошибку и рассчитать необходимую коррекцию коэффициентов сети но не делать эту коррекцию, и уже после подачи всех данных рассчитать сумму в корректировке каждого коэффициента сети сумма градиентов и произвести коррекцию коэффициентов на один шаг. Очевидно, что при большом наборе обучающих данных алгоритм будет работать крайне медленно, поэтому на практике часто производят корректировку коэффициентов сети после каждого элемента обучения, где значение градиента аппроксимируются градиентом функции стоимости, вычисленном только на одном элементе обучения. Такой метод называют стохастическим градиентным спуском или оперативным градиентным спуском. Стохастический градиентный спуск является одной из форм стохастического приближения. Теория стохастических приближений дат условия сходимости метода стохастического градиентного спуска. Акулич И. Математическое программирование в примерах и задачах. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация Practical Optimization. М., Коршунов Ю. Математические основы кибернетики. А., Филлиповская Е. Алгоритмы решения задач нелинейного программирования. Алгоритмы линейного и дискретного программирования. Справочник по математике для научных работников и инженеров. Городецкий, В. Нелинейное программирование и многоэкстремальная оптимизация.